 Widok zawartości stron
Widok zawartości stron
 Widok zawartości stron
Widok zawartości stron
 Widok zawartości stron
Widok zawartości stron
Czy Wszechświat jest komputerem kwantowym?

Każdą informację, z jaką każdego dnia się stykamy, da się sprowadzić do ciągu dwóch różnych symboli - 0 i 1. W ciągłych metamorfozach informacji wspierają ją komputery, będące w stanie w pewnym sensie za pomocą ciągu zer i jedynek "przeliczać rzeczywistość". Jednakże taka reprezentacja informacji zupełnie nie radzi sobie w mikroświecie, rządzonym przez prawa mechaniki kwantowej. Aby symulować rzeczywistość kwantową, trzeba sięgnąć po coś więcej, niż klasyczną maszynę - komputer kwantowy. O komputerach kwantowych, policzalności Wszechświata i o tym, czy nasza rzeczywistość to prawda, czy może tylko symulacja pisze dr hab. Jakub Mielczarek z Wydziału Fizyki, Astronomii i Informatyki Stosowanej UJ.
Oryginalny tekst znajduje się na blogu dr. hab. Jakuba Mielczarka.
Każdą informację z jaką mamy na co dzień do czynienia daje się sprowadzić do ciągu dwóch różnych symboli, na przykład kropek i kresek, jak w alfabecie Morse’a. Możemy zatem stwierdzić że, informacja podobnie jak materia posiada strukturę ziarnistą z „elementarną cząstką informacji” zwaną bitem. Do oznaczania dwóch możliwych wartości bitu, przyjęło się powszechnie używać 0 i 1. W szczególności, każdą liczbę naturalną możemy reprezentować jako skończony ciąg binarny. A zatem, rok założenia Uniwersytetu Jagiellońskiego to jak łatwo zapamiętać 010101010100 (pięć 01 i 00). W pewnym sensie, o tym, że również ułamki można reprezentować w podobny sposób zdawano sobie sprawę dużo wcześniej, bo już w starożytnym Egipcie. Nie tylko liczby ale także litery, znaki specjalne, obrazy i inne znane nam formy informacji dają się zakodować za pomocą zer i jedynek.
Informacja nie jest z reguły statyczna lecz podlega ciągłym metamorfozom w czym, za pomocą reprezentacji bitów jako impulsów elektrycznych, pomagają jej komputery. Komputery to zaś nic innego jak pewne układy fizyczne. Podążając tym tropem, możemy dojść do wniosku, że w zasadzie każdy wycinek rzeczywistości jest pewnego rodzaju komputerem, przetwarzającym lub przynajmniej przechowującym określony rodzaj informacji. Ale czy aby na pewno tak jest? Czy każdemu procesowi fizycznemu odpowiada przetworzenie informacji z którym poradziłby sobie komputer? Czy też ogólniej, czy nasza rzeczywistość jest obliczalna?
Próbę zmierzenia się z tymi z pozoru czysto filozoficznymi pytaniami podjął w latach trzydziestych ubiegłego wieku brytyjski matematyk, kryptolog i zdecydowanie wszechstronny geniusz Alan Turing. Analizując problem obliczalności różnych problemów, wprowadził on abstrakcyjny model maszyny obliczeniowej, nazwany później od jego nazwiska maszyną Turinga. Maszyna Turinga to idealizacja „matematyka” który, bit po bicie, dokonuje przetwarzania informacji zapisanej jako ciąg binarny na nieskończenie długiej taśmie.
Choć może to brzmieć zaskakująco, wszystkie operacje wykonywane przez współczesne komputery można przeprowadzić za pomocą maszyny Turinga, którą faktycznie da się zbudować, na przykład z klocków LEGO.

Maszyna Turinga zbudowana z klocków LEGO. Źródło.
Choć ta nie dostarcza optymalnego sposobu przetwarzania informacji, rozważania na jej temat pozwoliły wniknąć w naturę tego co obliczalne a co nie. Mianowicie, na kanwie rozważań Turinga, amerykański matematyk Alonzo Church sformułował hipotezę którą, w jednej ze swoich wcieleń, możemy wyartykułować następująco: Każde obliczenie (przetworzenie informacji) wykonane przez układ fizyczny (czyli układ spełniający prawa fizyki) możne zostać wykonane za pomocą maszyny Turinga.
Ta tak zwana hipoteza Churcha-Turinga ma doniosłe znaczenie z punktu widzenia symulowania procesów fizycznych. Procesy które mają reprezentację w postaci operacji wykonywalnych na maszynie Turinga, określamy mianem zupełnych w sensie Turinga. Otwartym problemem jest to czy wszystkie zjawiska fizyczne cechują się taką zupełnością i szczerzej czy cały Wszechświat można uznać za będący zupełnym w sensie Turinga. Choć, jak dotąd, nie przedstawiono kontrprzykładu dla hipotezy Churcha-Turinga, nie mamy jednak całkowitej pewności. Warto dodać, że zupełność Wszechświata implikuje to, że pewne problemy o których wiemy, że nie są zupełne w sensie Turinga, nie będą mogły zostać nigdy rozwiązane.
Poszukiwanie odpowiedzi na pytanie o zupełność Wszechświata w sensie Turinga komplikuje fakt, że reprezentacja informacji za pomocą ciągu zer i jedynek wymaga rewizji, kiedy zanurzymy się do mikroświata. Tam, w świecie rządzonym przez prawa mechaniki kwantowej, klasyczna teoria informacji uogólnia się do tak zwanej teorii informacji kwantowej. Podstawową jednostką informacji kwantowej jest zaś nie bit lecz kubit (ang. qubit). Kubit można wyobrazić sobie jako sferyczną powierzchnię Ziemi, na której biegunach znajdujemy klasyczne wartkości bitu 0 i 1. Kubit może jednak „żyć” nie tylko na biegunach ale w dowolnym innym punkcie, których na sferze (którą nazywamy sferą Blocha) jest nieskończenie wiele. Każdy z tych punktów jest tak zwaną kwantową superpozycją wartości klasycznych 0 i 1. Stany bardziej złożonych układów kwantowych nie reprezentujemy zaś jako ustalony ciąg bitów np. 011, lecz jako superpozycję wszystkich możliwych ciągów bitów o danej długości, w tym przypadku są to: 000, 001, 010, 100, 011, 101, 110 i 111. W ogólności zaś, dla układu kwantowego opisywanego przez n kubitów, stan kwantowy będzie superpozycją 2 do potęgi n ciągów binarnych, każdy o długości n bitów.

Geometryczna reprezentacja bitu i kubitu. Źródło.
Przetwarzanie informacji kwantowej jest, do pewnego stopnia, możliwe za pomocą komputerów klasycznych, a więc i za pomocą maszyny Turinga. Jest to jednak w ogólności zadanie karkołomne, gdyż dla n-kubitowego układu kwantowego wymaga to wykonania operacji na 2n amplitudach prawdopodobieństwa, każdego z możliwych ciągów n bitowych. Każdej z tych amplitud odpowiada zaś tak zwana liczna zespolona (złożona z dwóch liczb rzeczywistych), która może być reprezentowana przez ciąg bitów, o długości rosnącej wraz z dokładnością obliczeń. W konsekwencji, już dla stosunkowo małego układu kantowego złożonego ze stu kubitów potrzebujemy (w ogólnym przypadku) wykonać operacje na 2100 = 1267650600228229401496703205376 amplitudach, co jest poza zasięgiem jakichkowiek dostępnych obecnie, jak i możliwych do wyobrażenia sobie przyszłych, komputerów klasycznych.
W konsekwencji, symulowanie rzeczywistości kwantowej za pomocą maszyny klasycznej jest skrajnie nieefektywne. Wyjściem z tego impasu jest uogólnienie maszyny Turinga do przypadku kwantowego, będącej modelem nie komputera klasycznego lecz uniwersalnego komputera kwantowego. Idea takich maszyn pojawiła się w pierwszej połowie lat osiemdziesiątych ubiegłego wieku za sprawą fizyków Paula Benioffa i Davida Deutscha. Niemal równocześnie, amerykański fizyk którego nie trzeba nikomu przedstawiać — Richard Feynman, zaproponował, że każdy dyskretny układ kwantowy może być symulowany w sposób dokładny (może być “imitowany”) za pomocą operacji wykonywanych na komputerze kwantowym. Ekstrapolując to rozumowanie, jeśli więc Wszechświat da się zredukować do pewnego skończonego układu kubitów to będzie on zupełny w sensie kwantowej maszyny Turinga. Innymi słowy, możemy wtedy powiedzieć, że będzie on przykładem uniwersalnego komputera kwantowego.
Czy Wszechświat jest w istocie gigantycznym komputerem kwantowym nieustannie przetwarzającym informację kwantową? Tego wciąż nie wiemy. Natomiast, nasze obecne zrozumienie fizyki na najbardziej podstawowym poziomie do którego sięga nasza wiedza i wyobraźnia, nie wyklucza takiej możliwości. Tę granicę naszego dotychczasowego poznania określamy mianem skali Plancka, a na fizykę którą staramy się ją opisać składa się szereg propozycji kwantowych teorii grawitacji. Jedną z najpopularnieszych z nich jest teoria pętlowej grawitacji kwantowej, którą na początku lat dziewięćdziesiątych ubiegłego wieku wprowadzili Abhay Ashtekar, Carlo Rovelli i Lee Smolin. Teoria ta przewiduje, że przestrzeń na skali Plancka posiada dyskretną (“atomową”) postać, teoretycznie pozwalając na wykonanie jej symulacji kwantowych, w duchu idei Feynmana.
Nad tym jak zredukować pętlową grawitację kwantową do układu kubitów, co umożliwiłoby przeprowadzenie kwantowych symulacji, rozmyślam już od około dekady. Jednakże dopiero około trzech lat temu zabrałem się za podjęcie próby faktycznego urzeczywistnienie tego pomysłu. Impulsem do tego był fakt pojawienia się pierwszych dostępnych komputerów kwantowych, operujących na kilku i kilkunastu kubitach. W toku badań, które obecnie prowadzimy w ramach działajacego w Instytucie Fizyki Teoretycznej UJ zespołu Quantum Cosmos Lab, udało się nie tylko teoretycznie wykazać możliwość prowadzenia kwantowych symulacji modeli Wszechświata opisywanych przez pętlową grawitację kwantową, ale również wykonać pierwsze symulacje kwantowe tego typu.
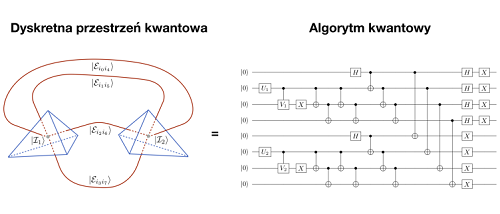
Model dyskretnej przestrzeni kwantowej zbudowanej z dwóch “atomów przestrzeni”
(lub równoważnie dipolowe przybliżenie Wszechświata) oraz odpowiadający mu algorytm kwantowy,
który można wykonać na kwantowej maszynie Turinga. Źródło.
Symulacje te, z uwagi na ograniczenia współczesnych pierwszych komputerów kwantowych są wciąż prymitywne i wykorzystują maksymalnie kilkanaście „nieoszlifowanych” kubitów. Pozwala to jednak na wytworzenie konfiguracji opisujących jednorodny model Wszechświata. Wraz z rozwojem inżynierii obliczeń kwantowych będziemy mogli temu mikroskopijnemu wszechświatowi dodawać coraz więcej upiększeń. Bazując na prognozach, już w przeciągu najbliższych pięciu lat możemy spodziewać się osiągnięcia poziomu symulacji z którymi nie poradzą sobie dostępne superkomputery klasyczne. Wykorzystanie klasycznej maszyny Turinga pozostanie wciąż teoretycznie możliwe lecz, z uwagi na jej skrajną nieefektywność, w praktyce niewykonalne. Otrzymana kwantowa symulacja wszechświata będzie jednak nadal jedynie kwantowym zarodkiem tego w którym żyjemy.
Spoglądając tysiące lat w niepewną przyszłość, nie możemy wykluczyć, że pełne symulacje makroskopowych wycinków Wszechświata staną się faktem. Nawet najbardziej zaawansowana symulacja nie będzie jednak w stanie odtworzyć w pełni Wszechświata w którym jesteśmy zanurzeni. Chyba, że w hipotetycznym przypadku granicznym kiedy to on cały zostałby wykorzystany do tego by symulować samego siebie. Ale to nie byłaby już symulacja, lecz to co nazywamy rzeczywistością i to na dodatek zupełną w sensie Turinga.
dr hab. Jakub Mielczarek
Wydział Fizyki, Astronomii i Informatyki Stosowanej UJ
Bibliografia:
[1] J. Mielczarek, Quantum Gravity on a Quantum Chip, arXiv:1803.10592 [gr-qc].
[2] J. Mielczarek, Spin Foam Vertex Amplitudes on Quantum Computer – Preliminary Results, Universe 5 (2019) no.8, 179 [arXiv:1810.07100 [gr-qc]].
[3] G. Czelusta, J. Mielczarek, Quantum simulations of a qubit of space, arXiv:2003.13124 [gr-qc].


![Pszczoły na diecie? [wideo]](/documents/74541952/147053668/bee2_230x300.png/132b8ed5-2598-4f5d-a105-c565636e3911?t=1616428310238)