
5 lipca bieżącego roku, amerykański Narodowy Instytut Norm i Techniki (National Institute of Standards and Technology - NIST) ogłosił pierwsze wyniki zainicjowanej w 2016 roku procedury wyłonienia postkwantowych standardów kryptograficznych. Wybrano jeden algorytm wymiany klucza oraz trzy algorytmy podpisu elektronicznego. W oparciu o te algorytmy, zostaną opracowane nowe standardy kryptograficzne, zapewniające odporność na możliwe przyszłe ataki przeprowadzane z udziałem komputerów kwantowych.
Dostępnym obecnie komputerom kwantowym daleko jeszcze do osiągnięcia zdolności umożliwiających skuteczną kryptoanalizę stosowanych współcześnie algorytmów szyfrujących. Niemniej jednak, zagrożenie takie, choć odsunięte w czasie, teoretycznie istnieje i należy je brać pod uwagę w analizie ryzyka. Problem ten dotyczy głównie algorytmów kryptografii klucza publicznego (kryptografii asymetrycznej), w których szyfrowanie i deszyfrowanie odbywa się za pomocą dwóch różnych kluczy: prywatnego i publicznego. Wykorzystując kryptoanalizę kwantową, możliwe staje się efektywne obliczeniowo odzyskiwanie klucza prywatnego w oparciu o znajomość klucza publicznego. Do przykładów kryptografii klucza publicznego należą algorytm RSA (Rivest-Shamir-Adleman), algorytmy kryptografii krzywych eliptycznych (Elliptic Curve Cryptography - ECC) oraz protokół uzgadniania klucza Diffiego-Hellmana (DH) (także w wersji opartej na krzywych eliptycznych, czyli tzw. Elliptic Curve Diffie-Hellman - ECDH).
Jednym z głównych zastosowań tych algorytmów jest zdalna wymiana sekretnego klucza, służącego następnie do zaszyfrowania wiadomości (tekstu jawnego), już za pomocą algorytmów symetrycznych. W przypadku szyfrów symetrycznych, ten sam klucz jest wykorzystywany do szyfrowania i odszyfrowania wiadomości.

Artystyczna wizja komputera kwantowego Sycamore firmy Google. Źródło
Opisana procedura znajduje szerokie zastosowanie w bezpiecznej wymianie informacji, w tym tych które możemy scharakteryzować jako szczególnie wrażliwe. Co więcej, część tego typu informacji może pozostać wrażliwa przez długi okres czasu, liczony w dziesiątkach lat. Stąd też istnieje uzasadniona obawa, że informacje te (w postaci zaszyfrowanej) mogą zostać przechowywane przez okres nawet kilkudziesięciu lat, po czym zostaną skutecznie odczytane z zastosowaniem kryptoanalizy kwantowej - łamiąc szyfry asymetryczne i uzyskując dostęp do klucza szyfrującego właściwą informację. Warto dodać, że nie pomoże tu nawet własność tzw. utajniania z wyprzedzeniem (ang. forward secrecy), stosowana dziś powszechnie w szyfrowaniu ruchu w internecie.
W świetle potencjalnego kryzysu jaki taka sytuacja mogłaby wywołać, społeczność kryptologiczna podjęła działania mające na celu opracowanie zbioru rozwiązań kryptograficznych odpornych na znane ataki z wykorzystaniem komputerów kwantowych. Właśnie tę gałąź kryptografii określamy mianem kryptografii postkwantowej (ang. post-quantum cryptography - PQC) [1].
O ile, w świetle obecnego stosunkowo wolnego tempa wzrostu zasobów obliczeniowych komputerów kwantowych i wielu przeszkód technicznych związanych ze skalowaniem procesorów kwantowych, szerokie wprowadzanie kryptografii postkwantowej może stwarzać wrażenie działań nieco przedwczesnych, należy mieć na uwadze złożoność i długotrwałość procesu opracowania, testowania, standaryzacji i szerokiej implementacji algorytmów postkwantowych. Fizyk kwantowy Michele Mosca, ujął ten problem w ramach następującej nierówności [2]: x+y>z, gdzie x to wymagany przez nas czas zapewnienia bezpieczeństwa informacji, y to czas wdrożenia nowych rozwiązań zapewniających bezpieczeństwo przed atakami kwantowymi, z to czas potrzebny na powstanie komputera zdolnego do łamania obecnych szyfrów kryptografii klucza publicznego. Jeśli powyższa nierówność zachodzi, to musimy uznać sytuację za problematyczną.
Oczywiście, dużą niepewnością obarczone jest wyznaczenie wartości parametru z. W niniejszym artykule, koncentruję uwagę na kryptografii postkwantowej i nie jest to miejsce na wnikliwą analizą aspektów fizycznych i technicznych stojących za prognozowaniem wartości parametru z. Uproszczona analiza, przedstawiona w moim wcześniejszym artykule pt. “Technologie kwantowe a cyberbezpieczeństwo” [3], wskazuje na to, że wartość z może wynosić obecnie około 25 lat. Realistycznie, możemy przyjąć, że szerokie wdrożenie standardów postkwantowych zajmie około 10 lat. Zastosowanie tych wartości do nierówności Mosca, prowadzi do wyrażenia: x > 15 lat. Oznacza, to że wymiana w internecie informacji, którymi nie chcielibyśmy się publicznie dzielić przez okres większy niż 15 lat, przestanie być bezpieczna pod koniec okresu adaptacji kryptografii postkwantowej. Rozważając bardziej optymistyczne scenariusze rozwoju technologii kwantowych, wartość ta ulegnie obniżeniu. Jednakże, już przytoczone tu ograniczenie, stanowi poważne ostrzeżenie w świetle wymiany informacji medycznych, biznesowych czy też komunikacji rządowej.
Konkursy NIST
W styczniu 1977 roku, amerykańskie Narodowe Biuro Standardów (ang. National Bureau of Standards), które w 1988 roku zostało przemianowane w NIST, opublikowało pierwszy powszechnie stosowany standard kryptografii symetrycznej - Digital Encryption Standard (DES). Pomimo wyłonienia projektanta algorytmu na drodze konkursowej, którym został IBM, proces standaryzacji nie przebiegł w sposób transparentny i jego wyniki szybko wzbudziły kontrowersje w środowisku kryptologicznym. Stało się to, w szczególności, za sprawą stosunkowo krótkiego, 56-bitowego, klucza. Na jego długość, jak dzisiaj wiemy, wpływ miała amerykańska National Security Agency (NSA), zaangażowana w przebieg procesu opracowania standardu DES [4]. W konsekwencji, już po dwudziestu latach od wprowadzenia szyfru DES, jego łamanie metodą siłową (ang. brute force) nie nastręczało większych problemów. DES stał się tym samym bezużyteczny (poza jego wykorzystaniem m.in. w algorytmach 3DES czy też DES-X) a NIST rozpoczął procedurę wyboru szyfru blokowego, stanowiącego nowy standard kryptografii symetrycznej. Tym razem jednak, w celu uniknięcia wcześniejszych kontrowersji (związanych również z pochodzeniem tak zwanych S-bloków, stanowiących element budulcowy algorytmu DES), zdecydowano się na w pełni otwartą i transparentną procedurę konkursową. Tak też wyłoniono algorytm Rijndael, który przybrał formę nowego standardu - Advanced Encryption Standard (AES), przyjętego w 2001 roku i obowiązującego do dzisiaj. Co więcej, w wersji z kluczem 256 bitowym jest on klasyfikowany jako algorytm postkwantowy.
W przeciągu ostatnich dwudziestu lat NIST opracował dziesiątki standardów i rekomendacji dotyczących algorytmów kryptograficznych, m.in. dotyczących funkcji skrótu (funkcji haszujących), podpisów elektronicznych, czy też generatorów kluczy. Do najnowszych inicjatyw NIST w zakresie standaryzacji kryptografii należą standardy lekkiej kryptografii (ang. lightweight cryptography), dedykowane dla urządzeń o ograniczonych zasobach obliczeniowych (mikrokontrolery, rozwiązania IoT, itp.), oraz dyskutowana tutaj standaryzacja kryptografii postkwantowej [5].

Artystyczne ujęcie drzewa Markle'a (stosowanego do etapu etapowania w algorytmie
podpisu elektronicznego na figurze skrótu) oraz krat. Źródło
Procedura wyłonienia standardów kryptografii postkwantowej została zainicjowana w grudniu 2016 roku. Ogłoszony przez NIST konkurs dotyczył wyboru postkwantowego algorytm kryptografii klucza publicznego, mechanizmu enkapsulacji klucza (ang. Key Encapsulation Mechanism - KEM) oraz podpisu elektronicznego. Określono, pięć poziomów bezpieczeństwa dla algorytmów postkwantowych, odpowiadających bezpieczeństwu ze względu na ataki siłowe na szyfr blokowy z kluczem o długości 128, 192 i 256 bitów oraz ze względu na ataki kolizyjne na funkcje skrótu ze skrótem 256 i 384 bitowym. Dalsze, szczegółowe informacje dotyczące wymogów stawianych przed kandydatami zainteresowany Czytelnik znajdzie w dokumencie [6].
Warte podkreślenia, jest, że nowe standardy kryptografii postkwantowej odchodzą od protokołu uzgadniania klucza DH, w którym uczestniczą dwie komunikujące się strony. Nie przewiduje się zatem postkwantowej wersji protokołu Diffiego-Hellmana. Jako alternatywę przyjęto natomiast wspomnianą enkapsulację klucza, w której jedna ze stron wybiera sekretny klucz i dokonuje jego zaszyfrowania postkwantowym algorytmem asymetrycznym, wykorzystując klucz publiczny. Zaszyfrowany klucz jest następnie odzyskiwany przez drugą stronę, za pomocą klucza prywatnego. Rozwiązanie takie uznano za prostsze i łatwiejsze do implementacji i analizy [7].
Warto również podkreślić, że konkurs NIST nie obejmuje nowych standardów funkcji skrótu. Te obecnie stosowane (np. SHA-3) uważane są za odporne na ataki kwantowe. Dzięki temu, znajdują one także zastosowanie w postkwantowych algorytmach podpisu elektronicznego, opartych na funkcjach skrótu (ang. Hash-based signatures).
Postkwantowi zwycięzcy
Z przesłanych wyjściowo osiemdziesięciu dwóch propozycji, po zakończonej trzeciej rundzie, wyłoniono cztery algorytmy. Ponadto, cztery kolejne, zostały zakwalifikowane do, następnej, czwartej rundy [8].
Jako algorytm kryptografii klucza publicznego wyłoniony został CRYSTALS-Kyber [9]. Algorytm ten zapewnia również mechanizm enkapsulacji klucza (KEM). CRYSTALS-Kyber należy do klasy szyfrów kratowych (ang. lattice-based cryptography) [10], w których operacje wykonywane są na wielowymiarowych kratach, podobnych do sieci krystalicznych. Kraty dają możliwość zdefiniowania szeregu problemów, które uważane są za trudne obliczeniowo. Jednym z nich jest problem nauczania z błędami (ang. Learning With Errors - LWE), który w 2005 roku, zaproponował izraelski informatyk-teoretyk Oded Regev. Za swoje odkrycie został On w 2018 roku uhonorowany prestiżową Nagrodą Gödla. Algorytm CRYSTALS-Kyber bazuje na wariancie problemu LWE, w którym krata definiująca problem posiada pewną narzuconą strukturę, tzw. Module-LWE. W uzasadnieniu wyboru tego algorytmu, NIST podkreślił m.in. jego szybkość oraz nieduży rozmiar kluczy, rzędu kilobajta.
Jako algorytmy podpisu elektronicznego zostały wyłonione: CRYSTALS-Dilithium [9], FALCON [11] oraz SPHINCS+ [12]. CRYSTALS-Dilithium, został zaprojektowany przez tę samą grupę co CRYSTALS-Kyber i uznano go za główny algorytm postkwantowego podpisu elektronicznego. Algorytm CRYSTALS-Dilithium oparty został na modyfikacji problemu LWR, tak zwanej nauce z zaokrągleniem (ang. Learning With Rounding - LWR). W problemie tym, zamiast dodawania szumu gaussowskiego (jak w LWE), wprowadza się funkcję zaokrąglającą, utrudniającą odzyskanie sekretnej wiadomości. Co więcej, podobnie jak CRYSTALS-Kyber, tak i CRYSTALS-Kyber, wykorzystuje narzuconą strukturę kraty, co ostatecznie prowadzi do problemu Module-LWR.
Przyszły standard FALCON opiera się na dobrze zbadanym algorytmie NTRU, który w swojej pierwszej wersji, został wprowadzony w 1996 roku [13]. Algorytm jest uznawany za protoplastę szyfrów kratowych. Jest on szybki oraz łatwy w implementacji. O ile wyjściowo, jego działanie można zrozumieć nie odwołując się do krat - bazuje on mianowicie na operacjach wykonywanych na tzw. pierścieniach ilorazowych wielomianów - to już istota jego bezpieczeństwa bezpośrednio wynika z własności krat. Pomimo stosunkowo małych rozmiarów klucza, słabą stroną szyfru FALCON jest brak realizacji stałoczasowej, odpornej na ekstrahowanie klucza prywatnego z pomiaru czasu działania algorytmu. Kolejnym kłopotem jest wymagana szybka arytmetyka o podwójnej precyzji, utrudniająca implementację tego szyfru [14].
W odróżnieniu od wcześniejszych przypadków, szyfr SPHINCS+ nie jest oparty na matematyce krat. Został on wyłoniony przez NIST jako algorytm rezerwowy, na wypadek gdyby czas odsłonił nieznane dotychczas podatności szyfrów kratowych. A o tym, że faktycznie może się tak zdarzyć, piszę w dalszej części tego tekstu. Póki co, należy jeszcze dodać, że algorytm SPHINCS+ opiera się na dobrze poznanych i silnych kryptograficznie funkcjach skrótu. Idea wykorzystania funkcji skrótu do składania podpisu, została zaproponowane jeszcze w 1975 roku przez amerykańskiego informatyka Leslie Lamporta. W podejściu tym, klucz prywatny jest zużywany do tworzenia kluczy publicznych, poprzez utworzenie funkcji skrótu z części jego bitów. W konsekwencji, praktyczne zastosowania algorytmów podpisu elektronicznego opartych na funkcjach skrótu wymagają zastosowania dużych kluczy, których rozmiary mogą sięgać kilkudziesięciu kilobajtów. Jest to główny mankament tego podejścia. Poza tym, algorytmy te są zarówno bezpieczne, jak i łatwe w implementacji, gdyż opierają się na dobrze przetestowanych i szeroko wdrożonych rozwiązaniach.
Kontrowersje na finiszu
4 kwietnia bieżącego roku, na 3 miesiące przed ogłoszeniem wyników przez NIST, kryptolodzy z prestiżowego Center of Encryption and Information Security (MATZOV), będącego głównym zapleczem kryptologicznym Izraela, zatrzęśli światem kryptologicznym, a przynajmniej jego postkwantową częścią, publikując swój raport, będący wynikiem przeprowadzonego audytu głównych kandydatów do standardu kryptografii postkwantowej. Raport zatytułowany jest “Report on the Security of LWE: Improved Dual Lattice Attack” i skupia uwagę na podejściach opartych na LWE oraz LWR [15]. Najlepiej znane techniki kryptoanalityczne dla tego typu szyfrów opierają się na podejściach zwanych primal lattice attacks oraz dual lattice attacks. Żaden z tych ataków nie uważano jednak dotychczas za realne zagrożenie. W szczególności, drugie z tych podejść wydawało się niepraktyczne. E W raporcie MATZOVa wykazano jednak, że istnieje możliwość ulepszenia drugiego typu ataku, co wyraźnie osłabia bezpieczeństwo algorytmów CRYSTALS-Kyber, SABER oraz CRYSTALS-Dilithium. W szczególności, wykazano, że nowa technika kryptoanalityczna osłabia bezpieczeństwo tych algorytmów nieznacznie poniżej progów określonych w wymaganiach konkursowych NIST. Czytelnika zainteresowanego dyskusją środowiska kryptologów postkwantowych na temat raportu MATZOVa odsyłam do referencji [16].
Wyniki raportu MATZOVa ostatecznie nie przeszkodziły w wyborze algorytmów CRYSTALS-Kyber i CRYSTALS-Dilithium. Mogły mieć jednak wpływ na odrzucenie z rywalizacji algorytmu SABER. Warto w tym miejscu wyjaśnić, że nie dysponujemy dowodem bezpieczeństwa algorytmów CRYSTALS-Kyber i CRYSTALS-Dilithium. Stwierdzenia dotyczące ich bezpieczeństwa wiążą się z tzw. problemem najkrótszego wektora (ang. Shortest Vector Problem - SVP) na kratach [17]. Jak dowiedziono, SVP jest tzw. problemem NP-trudnym, co uniemożliwia jego efektywne rozwiązywania (w czasie wielomianowym). Problemy LWE i LWR można zredukować do przybliżonego problemu SVR. Nie istnieje jednakże dowód tego, że są to problemy NP-trudne. Od strony bezpieczeństwa, uzasadnienie zastosowania tych problemów w kryptografii postkwantowej opiera się więc na braku znajomości algorytmów które pozwalałyby na efektywne rozwiązywanie tych problemów. Nie można jednak zagwarantować tego, że takie algorytmy nie zostaną odkryte w przyszłości.
Czwarta runda
Proces wyboru postkwantowych standardów kryptograficznych przez NIST, nie zakończył się wraz z wyborem omówionych powyżej czterech algorytmów. Gra toczy się dalej i do czwartej rundy ewaluacyjnej zakwalifikowano cztery kolejne algorytmy, które wciąż mają szansę dołączyć do grona postkantowych standardów NIST. Mowa to szyfrach: BIKE [18], Classic McEliece [19], HQC [20], oraz SIKE [21].
Zacznijmy od przedstawienia drugiego z listy, szyfru Classic McEliece, należącego do klasy szyfrów asymetrycznych opartych na kodach korekcyjnych. Kody takie, poprzez pewną nadmiarową informację, pozwalają na korekcję błędów powstałych w trakcie transmisji lub magazynowania informacji. W 1978 roku Robert McEliece pokazał, że kody korekcyjne mogą być również użyte do realizacji, wprowadzonej kilka lat wcześniej, kryptografii asymetrycznej. Pomimo, ponad czterdziestu lat prób i dogłębnego poznania algorytmu, nie udało się przeprowadzić na niego skutecznego ataku. Słabą stroną algorytmu jest duży rozmiar klucza - nawet rzędu megabajta. Algorytm BIKE (Bit Flipping Key Encapsulation) jest, podobnie jak Classic McEliece, również oparty na kodach korekcyjnych. W tym przypadku wykorzystywany jest tzw. kod QC-MDPC (Quasi-Cyclic Moderate Density Parity-Check). Także algorytm HQC (Hamming Quasi-Cyclic) opiera swoje działanie na kodach korekcyjnych.
Ostatni z szyfrów, SIKE (Supersinguar Isogeny Key Encapsulation), wykorzystuje zupełnie inne podejście niż trzy poprzednie. A mianowicie, angażuje on morfizmy (pewne powiązania) pomiędzy krzywymi eliptycznymi do budowy kryptosystemu asymetrycznego. Podejście to, pomimo, że jest wymagające obliczeniowo, uważne było do niedawna za bezpieczne i charakteryzujące się wyjątkowo krótkim kluczem. Prognozowało to wykorzystaniem algorytmu SIKE, w obszarach zastosowań specjalnego przeznaczenia. Ku wielkiemu zaskoczeniu społeczności kryptologicznej, 30 lipca tego roku dwójka kryptologów z Uniwersytetu w Leuven, opublikowała receptę skutecznego ataku na algorytm SIKE [22,23]. Wykorzystując nieznaną wcześniej podatność, udało się, wykorzystując komputer osobisty, odzyskać klucz prywatny. Algorytm ten, pomimo wiązanych z nim nadziejami i już testowanych implementacji, nie stanie się z pewnością standardem postkwantowym. Wciąż możliwe jest jednak, że podatność która umożliwiła atak zostanie wyeliminowana w dalszych wcieleniach tego algorytmu.
Co z kryptografią symetryczną?
Współczesne algorytmy kryptografii symetrycznej są uważane za niepodatne na ataki kwantowe. Ich poziom bezpieczeństwa jest zasadniczo określany ze względu na atak siłowy, którego możliwość realizacji determinuje rozmiar przestrzeni klucza. W przypadku algorytmu AES z kluczem 256 bitowym, przestrzeń ta ma wymiar N=2256, co jest porównywalne z liczbą atomów w obserwowanym Wszechświecie.
Najlepszą znaną strategią kwantową w przypadku ataków siłowych jest zastosowanie algorytmu Grovera. Algorytm ten umożliwia przeszukanie kwantowej bazy danych, zawierającej N elementów, nie jak to ma miejsce klasycznie w średnio N/2 krokach, a w średnio N1/2 krokach. Dla algorytmu AES-256 oznacza to redukcję bezpieczeństwa z poziomu 256 do 128, co jest wciąż wartością uznawaną za bezpieczną postkwantowo. Ponadto, należy podkreślić, że już od strony teoretycznej, samo zaimplementowanie algorytmu przeszukiwania Grovera dla danego algorytmu symetrycznego stanowi duże wyzwanie. Trzeba mianowicie zbudować obwód tzw. kwantowej wyroczni (ang. oracle) dla danego algorytmu symetrycznego. To samo w sobie złożone zadanie, wymagające dokonania reprezentacji danego algorytmy symetrycznego w postaci funkcji binarnej i jej dalszej implementacji jako obwodu kwantowego. Stanowi to ogromne wyzwanie już na poziomie algorytmicznym.
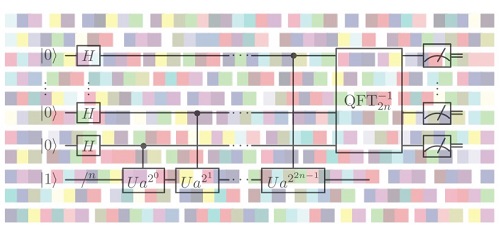
Obwód kwantowy dla algorytmu Shora na tle fragmentu książki Georga Orwella 1984,
zakodowanej za pomocą kolorów przez Hyo Myoung Kima [cała książka]
Zaproponowany przez Lova K. Grovera w 1996 algorytm był przez wielu uważany za jedyne kwantowe zagrożenie dla algorytmów symetrycznych. Spojrzenie na kryptoanalizę algorytmów symetrycznych uległo jednak zmianie w 2016 roku, wraz opublikowaniem publikacji pt. “Breaking Symmetric Cryptosystems Using Quantum Period Finding” [24]. Pokazano, mianowicie, że możliwe jest osiągnięcie tzw. przyśpieszenia wykładniczego dla kryptoanalizy pewnych algorytmów symetrycznych. Ma to miejsce za sprawą sprytnego zastosowania kwantowego algorytmu Simona, który jest prostszą wersją algorytmu Shora. Algorytm Shora stanowi zaś podstawowe zagrożenie dla algorytmów asymetrycznych.
Zastosowanie algorytmu Simona umożliwia, w szczególności, efektywną kryptoanalizę prostego szyfru blokowego, jakim jest algorytm Even-Mansoura. Choć algorytm Even-Mansoura jest zbyt prosty by mógł znaleźć praktyczne zastosowanie, jego warianty odnaleźć można w szyfrach lekkiej kryptografii. W szczególności, należą do nich algorytmy Chaskey i Elephant, będący jednym z finalistów procesu NIST standaryzacji kryptografii lekkiej.
Należy zauważyć, że kwantowa kryptoanaliza szyfrów symetrycznych staje się coraz bardziej aktywnym polem badań. Kwestii bezpieczeństwa szyfrów symetrycznych nie należy zatem bagatelizować.
Co dalej?
Jak deklaruje NIST, przygotowanie gotowych standardów na podstawie wybranych algorytmów może zająć kolejne dwa lata. W międzyczasie, agencja zachęca do poznawania i testowania wyłonionych algorytmów. NIST sugeruje również powstrzymanie się z praktycznymi implementacjami na tym etapie, gdyż finalna forma standardów może odbiegać od obecnej specyfikacji algorytmów. Czas ten warto niewątpliwie wykorzystać także na poszerzenie świadomości związanej z wdrażaniem kryptografii postkwantowej i przygotowanie się do działań jakie ogłoszenie nowych standardów pociągnie za sobą w nadchodzących latach. Dotyczy to, w szczególności, działów IT firm i instytucji. Uwagę na kwestię nowych standardów powinny niezwłocznie zwrócić podmioty działające w obszarach infrastruktury sieciowej, magazynowania danych oraz cyberbezpieczeństwa. Należy mieć także świadomość tego, że w przeciągu najbliższych kilku lat, każdy administrator sieciowy będzie musiał zaznajomić się z nowymi postkwantowymi wersjami protokołu TLS (Transport Layer Security) oraz oferowanymi przez nie postkwantowymi zestawami szyfrów (ang. cipher suites).
Czekamy, ponadto, na wyłonienie ewentualnych dodatkowych standardów, które będą mogły pełnić rolę rezerwową i specjalnego przeznaczenia. Z uwagi na przywołane niedawne doniesienia, z gry najprawdopodobniej wypadł już algorytm SIKE.
Nieodległy czas powinien przynieść również zainicjowanie procedury wyboru postkwantowego standardu szyfrowania homomorficznego (ang. homomorphic encryption). Szyfrowania tego typu zyskuje coraz większe zainteresowanie z uwagi na dynamiczny rozwój usług chmurowych. Kryptografia homomorficzna pozwala mianowicie na wykonywanie dowolnych operacji na zaszyfrowanych danych, nie mając do nich bezpośredniego dostępu.
-----
Autor:
Dr hab. Jakub Mielczarek - pracuje w Instytucie Fizyki Teoretycznej na Uniwersytecie Jagiellońskim, gdzie prowadzi zespół badawczy Quantum Cosmos Lab oraz hackerspace Garaż Złożoności. Wykłada m.in. Kryptografię oraz Matematykę Dyskretną.
----
Referencje:
[1] D. Bernstein, T. Lange, Post-quantum cryptography, Nature 549, 188–194 (2017).
[2] M. Mosca, Cybersecurity in an era with quantum computers: will we be ready ?, IEEE Security & Privacy, vol. 16, no. 5, pp. 38-41, (2018).
[3] J. Mielczarek, Technologie kwantowe a cyberbezpieczeństwo, CyberDefence24, (2019).
[4] T. R. Johnson, American Cryptology during the Cold War, 1945-1989 (The Complete Declassified Official Four-Volume History of the NSA), Center for Cryptologic History, Washington DC (1995) - Book III, Rozdział 19, Public Cryptography.
[5] https://www.nist.gov/cryptography
[7] https://blog.cloudflare.com/towards-post-quantum-cryptography-in-tls/
[10] https://itwiz.pl/czym-jest-szyfrowanie-kratowe-jak-zabezpiecza-czasach-quantum-computing/
[11] https://falcon-sign.info/
[12] https://sphincs.org/
[13] J. Hoffstein, J. Pipher, J. H. Silverman, NTRU: A ring-based public key cryptosystem. In: Buhler, J.P. (eds) Algorithmic Number Theory. ANTS 1998. Lecture Notes in Computer Science, vol 1423. Springer, Berlin, Heidelberg (1998).
[14] https://blog.cloudflare.com/nist-post-quantum-surprise/
[15] https://zenodo.org/record/6412487#.Yu2VuexBx4I
[16] https://groups.google.com/a/list.nist.gov/g/pqc-forum/c/Fm4cDfsx65s/m/v5odfcpfBwAJ?pli=1
[17]
http://www.deltami.edu.pl/temat/matematyka/kryptologia/2017/11/25/Kryptologia_postkwantowa/
[19] https://classic.mceliece.org/
[20] http://pqc-hqc.org/
[21] https://sike.org/
[22] W. Castryck and T. Decru, An efficient key recovery attack on SIDH (preliminary version) (2022)
[24] M. Kaplan., G. Leurent., A. Leverrier, M. Naya-Plasencia, Breaking Symmetric Cryptosystems Using Quantum Period Finding. In: Robshaw, M., Katz, J. (eds) Advances in Cryptology – CRYPTO 2016. CRYPTO 2016. Lecture Notes in Computer Science, vol 9815. Springer, Berlin, Heidelberg (2016).




